How the maps were generated
The maps were generated by subtracting predictions of ancient sea levels from the heights given in a global data set of present-day topography. The result is an estimate of the Earth's topography at the time the sea-level predictions relate to. The accuracy of the maps therefore depends on the veracity of the sea-level predictions as well as that of the adopted topography data set. We used the 5 minute Terrain Base elevation data set available from the National Geophysical Data Center . Go to this web site for more information on the accuracy of this data set. The sea-level model is based on a number of input parameters, some of which are better known than others. The largest error will result from uncertainties in the adopted ice model that drives the sea-level change, and the viscosity profile of the adopted earth model. The predictions from which the maps were derived are based on a revised version of the ICE-3G deglaciation history [Tushingham and Peltier, 1991] . The original ICE-3G model was revised to produce a good fit to the Barbados record and to include a glaciation phase [see, for example, Milne et al., 2002]. Details of the adopted earth model can also be obtained from the Milne et al. article. The earth model viscosity structure was chosen to be broadly consistent with a number of recent inferences. It is important to note that the sea-level model does not account for tectonic or sedimentary processes and so care should be taken when applying the maps in regions where these processes have a significant effect on sea-level change.
The fit of the sea-level model to the Barbados coral record is shown below.
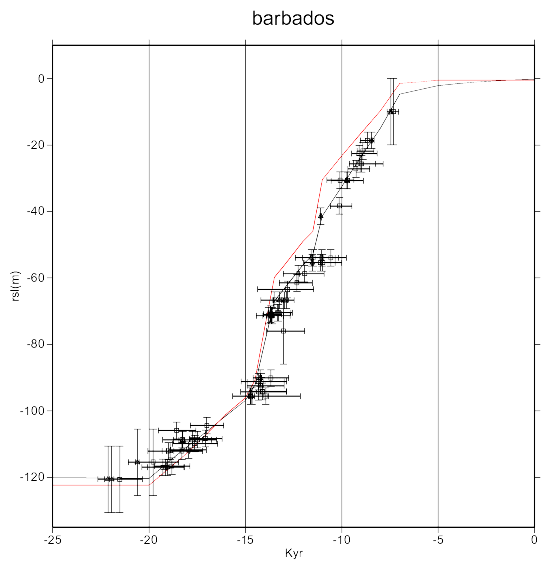
The solid black line shows the fit of the model to the Barbados data. The red line shows the eustatic or meltwater component of the model. This illustrates the rate that glacial meltwater is input to the global oceans during deglaciation. Note that this rate varies significantly between the last glacial maximum (around 20 kyr BP) and present. For example, these is a very large flux around 14 kyr BP. When looking at the palaeoshoreline maps, you will notice that there is a large change in shoreline geometry from 15 to 13 kyr BP due to this large meltwater influx. Note that all times given on this web site are calibrated kyr BP.
References
Tushingham, M.A. and W.R. Peltier, 1991. ICE-3G A new global model of late Pleistocene deglaciation based on geophysical predictions of post-glacial relative sea-level change, Journal of Geophysical Research, 96, 4497-4523.
Milne, G.A., J.X. Mitrovica and D.P. Schrag, 2002. Estimating past continental ice volume from sea-level data, Quaternary Science Reviews, 21, 361-376.

